Pada Bab sebelumnya kita telah membahas diferensial numerik. Nah, pada kesempatan kali ini kita akan membahas tentang integral menggunakan metode numerik. Untuk integral kali ini lebih ditekankan lagi kepada pengaplikasian perhitungan luas sebuah daerah. Ya seperti yang kita tau bahwa integral bisa juga digunakan untuk menghitung luas suatu wilayah.
Berikut beberapa poin tentang integral numerik :
- Integral numerik merupakan alat (cara) yang digunakan oleh ilmuwan untuk memperoleh jawaban hampiran (aproksimasi) dari pengintegralan yang tidak dapat diselesaikan secara analitik (memerlukan sumberdaya yang sangat banyak dalam penyelesaiannya).
- Penerapan integral: menghitung luas dan volume-volume benda putar.
- Melakukan penginteralan pada bagian-bagian kecil, dengan menjumlahkan bagian-bagian tersebut.
- Metoda Numerik mencoba untuk lebih cepat dan lebih mendekati jawaban eksak.
 |
| membagi kecil kemudian dijumlahkan |
Dalam Integral Numerik dikenal beberapa metode diantaranya :
- Metode Reimann
- Metode Trapezoida
- Metode Simpson 1/3
- Metode Simpson 3/8
1. Metode Reimann
Ide dari metode reimann adalah mempartisi sebuah fungsi sehingga lebih kecil yang berbentuk segi empat. kemudian dijumlahkan masing-masing partisi tersebut. ilustrasi : |
| Metode Reimann |
Luas Keseluruhan = L0+L1+...+Ln = f(x0).x0+f(x1).x1+...+f(xn).xn
Jika jarak antar partisinya(h) sama maka bisa disederhanakan menjadi :
Luas Keseluruhan = f(x0).h+f(x1).h+...+f(xn).h = h.(f(x0)+f(x1)+...+f(xn))
atau bisa ditulis dalam bentuk :
 |
| Rumus Metode Reimann(Komposit) |
Hitung luas daerah yang dibatasi oleh y = x2 dan sumbu x untuk x = [0,1] !
Jawab :
2. Metode Trapezoida
Idenya sama seperti reimann. Tetapi memodifikasi bentuk bangun datarnya yang tadinya segi empat menjadi trapesium. Ilustrasi : |
| Ilustrasi Metode Trapezoida |
 |
| Rumus Luas Trapesium, Sumber : HitungLuas.com |
Dengan keterangan sebagai berikut :
L = merupakan luas.
h = jarak antara x1 ke x0 (h = x1-x0).
f(x0) = tinggi di x0 (biasa kita kenal y0).
f(x1) = tinggi di x1 (biasa kita kenal y1).
Selanjutnya perhatikan gambar berikut :
 |
| Komposit Trapezoida |
"Semakin kecil nilai h, yang artinya semakin banyak partisi yang ada pada suatu fungsi maka semakin bagus pula hasil perhitungannya (mendekati nilai yang sebenarnya)".Nah, bagaimana sih cara menghitung luas tadi (yang diarsir biru). Maka kita tinggal menjumlahkan luas masing-masing partisi satu sama lain. Atau dalam matematikamya dituliskan demikian :
Atau kalau misalkan nilai h antar partisi sama, maka kita tinggal menyederhanakannya menjadi :
Mohon maaf apabila kekurangan dan kesalahan, semoga bermanfaat Terimakasih.
Selanjutnya ditunggu postingan yang membahas penggunaan metode ini ya.
Sumber :
Suryana Ino. 2016. Metode Numerik : Integrasi Numerik part 1 (PPT). Sumedang: Universitas Padjadjaran.
http://hitungluas.com/cara-menghitung-luas-trapesium-rumus-jumlah-sisi-sejajar-dibagi-dua-kali-tinggi (disadur dari berbagai sumber).



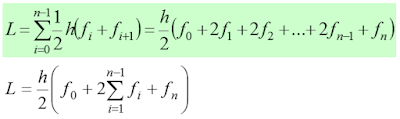
Posting Komentar untuk "Integral Numerik 1 (Reimann, Trapezoida)"
Berilah komentar, saran, dan kritik dengan bijak